Introduction
What is the period of oscillation T of a mass m attached to an ideal linear spring with spring constant k suspended in gravity of strength g? The four quantities have the following dimensions: T [T]; m [M]; k [M/T^2]; and g [L/T^2]. From these we can form only one dimensionless product of powers of our chosen variables, G₁ = Tk / m. The dimensionless product of powers of variables is sometimes referred to as a dimensionless group of variables, but the group, G₁, referred to means "collection" rather than mathematical group. They are often called dimensionless numbers as well.
Note that no other dimensionless product of powers involving g with k, m, T, and g alone can be formed, because only g involves L . Dimensional analysis can sometimes yield strong statements about the irrelevance of some quantities in a problem, or the need for additional parameters. If we have chosen enough variables to properly describe the problem, then from this argument we can conclude that the period of the mass on the spring is independent of g: it is the same on the earth or the moon. The equation demonstrating the existence of a product of powers for our problem can be written in an entirely equivalent way: , for some dimensionless constant κ.
When faced with a case where our analysis rejects a variable (g, here) that we feel sure really belongs in a physical description of the situation, we might also consider the possibility that the rejected variable is in fact relevant, and that some other relevant variable has been omitted, which might combine with the rejected variable to form a dimensionless quantity. That is, however, not the case here.
When dimensional analysis yields a solution of problems where only one dimensionless product of powers is involved, as here, there are no unknown functions, and the solution is said to be "complete."

A simple example
Consider the case of a vibrating wire of length l [L] vibrating with an amplitude A [L]. The wire has a linear density of ρ [M / L] and is under tension s [ML / T], and we want to know the energy, E, in the wire. Now we can easily find that we can form two dimensionless products of powers of the variables chosen, π₁ = E / As and . Perhaps surprisingly, like the g in the simple example given above, the linear density of the wire is not involved in either. The two groups found can be combined into an equivalent form as an equation

where F is some unknown function, or, equivalently as

where f is some other unknown function. Here the unknown function implies that our solution is now incomplete, but dimensional analysis has given us something that may not have been obvious: The energy is proportional to the first power of the tension. Barring further analytical analysis, we might proceed to experiments to discover the form for the unknown function f. But our experiments are simpler than in the absence of dimensional analysis. We'd perform none to verify that the energy is proportional to the tension. Or perhaps we might guess that the energy is proportional to 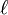, and so infer that . The power of dimensional analysis as an aid to experiment and forming hypotheses becomes evident.
The power of dimensional analysis really becomes apparent when it is applied to situations, unlike those given above, that are more complicated, the set of variables involved are not apparent, and the underlying equations hopelessly complex. Consider for example, a small pebble sitting on the bed of a river. If the river flows fast enough, it will actually raise the pebble and cause it to flow along with the water. At what critical velocity will this occur? Sorting out the guessed variables is not so easy as before. But dimensional analysis can be a powerful aid in understanding problems like this, and is usually the very first tool to be applied to complex problems where the underlying equations and constraints are poorly understood.

A more complex example
Huntley (Huntley, 1967) has claimed that it is sometimes productive to refine our concept of dimension. Two possible refinements are:
As an example of the usefulness of the first refinement, suppose we wish to calculate the distance a cannon ball travels when fired with a vertical velocity component V_y and a horizontal velocity component V_x, assuming it is fired on a flat surface. Assuming no use of directed lengths, the quantities of interest are then V_x, V_y, both dimensioned as L / T, R, the distance travelled, having dimension L, and g the downward acceleration of gravity, with dimension L / T
η the dynamic fluid viscosity with dimensions M / LT
r the radius of the pipe with dimensions L Huntley's addition
Huntley's addition has some serious drawbacks. It does not deal well with vector equations involving the cross product, nor does it handle well the use of angles as physical variables. It also is often quite difficult to assign the L, L_x, L_y, L_z symbols to the physical variables involved in the problem of interest. He invokes a procedure that involves the "symmetry" of the physical problem. This is often very difficult to apply reliably: it is unclear as to what parts of the problem that the notion of "symmetry" is being invoked. Is it the symmetry of the physical body that forces are acting upon, or to the points, lines or areas at which forces are being applied? What if more than one body is involved with different symmetries? Consider the spherical bubble attached to a cylindrical tube, where one wants the flow rate of air as a function of the pressure difference in the two parts. What are the Huntley extended dimensions of the viscosity of the air contained in the connected parts? What are the extended dimensions of the pressure of the two parts? Are they the same or different? These difficulties are responsible for the limited application of Huntley's addition to real problems.
Angles are conventionally considered to be dimensionless variables, and so the use of angles as physical variables in dimensional analysis can give less meaningful results. As an example, consider the projectile problem mentioned above. Suppose that, instead of the x- and y-components of the initial velocity, we had chosen the magnitude of the velocity v and the angle θ at which the projectile was fired. The angle is conventionally considered to be dimensionless, and the magnitude of a vector has no directional quality, so that no dimensionless variable can be composed of the four variables g, v, R, and θ. Conventional analysis will correctly give the powers of g and v, but will give no information concerning the dimensionless angle θ.
Siano (Siano, 1985-I, 1985-II) has suggested that the directed dimensions of Huntley be replaced by using orientational symbols to denote vector directions, and an orientationless symbol . Thus, Huntley's L_x becomes 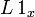with L  specifying the dimension of length, and 1_x specifying the orientation. Siano further shows that the orientational symbols have an algebra of their own. Along with the requirement that , the following multiplication table for the orientation symbols results: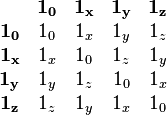

Note that the orientational symbols form a group (the Klein four-group or "viergruppe"). In this system, scalars always have the same orientation as the identity element, independent of the "symmetry of the problem." Physical quantities that are vectors have the orientation expected: a force or a velocity in the x-direction has the orientation of 1_x. For angles, consider an angle θ that lies in the z plane. Form a right triangle in the z plane with θ being one of the acute angles. The side of the right triangle adjacent to the angle then has an orientation 1_x and the side opposite has an orientation 1_y. Then, since tan(θ) = ly/lx = θ + ... we conclude that an angle in the xy plane must have an orientation 1_y/1_x = 1_z, which is not unreasonable. Analogous reasoning forces the conclusion that sin(θ) has orientation 1_z while cos(θ) has orientation 1₀. These are different, so one concludes (correctly), for example, that there are no solutions of physical equations that are of the form a sin(θ) + b cos(θ), where a and b are scalars.
The assignment of orientational symbols to physical quantities and the requirement that physical equations be orientationally homogeneous can actually be used in a way that is similar to dimensional analysis to derive a little more information about acceptable solutions of physical problems. In this approach one sets up the dimensional equation and solves it as far as one can. If the lowest power of a physical variable is fractional, both sides of the solution is raised to a power such that all powers are integral. This puts it into "normal form". The orientational equation is then solved to give a more restrictive condition on the unknown powers of the orientational symbols, arriving at a solution that is more complete than the one that dimensional analysis alone gives. Often the added information is that one of the powers of a certain variable is even or odd.
As an example, for the projectile problem, using orientational symbols, θ, being in the x-y plane will thus have dimension 1_z and the range of the projectile R will be of the form:
which means
Dimensional homogeneity will now correctly yield a=-1 and b=2, and orientational homogeneity requires that c be an odd integer. In fact the required function of theta will be sin(θ)cos(θ) which is a series of odd powers of θ.
It is seen that the Taylor series of sin(θ) and cos(θ) are orientationally homogeneous using the above multiplication table, while expressions like cos(θ) + sin(θ) and exp(θ) are not, and are (correctly) deemed unphysical.
It should be clear that the multiplication rule used for the orientational symbols is not the same as that for the cross product of two vectors. The cross product of two identical vectors is zero, while the product of two identical orientational symbols is the identity element.

Drawbacks and refinements: Orientational analysis
Ultimately, it can be seen that dimensional analysis and the requirement for physical equations to be dimensionally homogeneous reflects the idea that the laws of physics are independent of the units employed to measure the physical variables. That is, F = ma, for example, is true whether the unit system used is SI, English, or cgs, or any other consistent system of units. Orientational analysis and the requirement for physical equations to be orientationally homogeneous reflects the idea that the equations of physics must be independent of the coordinate system used.

Philosophical basis
The dimensionless constants that arise in the results obtained, such as the C in the Poiseuille's Law problem and the κ in the spring problems discussed above come from a more detailed analysis of the underlying physics, and often arises from integrating some differential equation. Dimensional analysis itself has little to say about these constants, but it is useful to know that they very often have a magnitude of order unity. This observation can allow one to sometimes make "back of the envelope" calculations about the phenomenon of interest, and therefore be able to more efficiently design experiments to measure it, or to judge whether it is important, etc.

Buckingham π theorem

Dirac large numbers hypothesis
Fundamental unit
Nondimensionalization
Equivalization
Physical quantity
Natural units
Similitude (model)
Buckingham π theorem
Units conversion by factor-label
Affine space which is like a vector space with no zero element and so models physical quantities more faithfully.