Babylonian mathematics refers to any mathematics of the peoples of
Mesopotamia (situated in present day
Iraq), from the days of the early
Sumerians to the fall of
Babylon in 539 BC. In contrast to the sparsity of sources in
Egyptian mathematics, our knowledge of
Babylonian mathematics is derived from some 400 clay tablets unearthed since the 1850s. Written in
Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include
fractions,
algebra,
quadratic and
cubic equations, the
Pythagorean theorem, and the calculation of
Pythagorean triples and possibly
trigonometric functions (see
Plimpton 322). The Babylonian tablet YBC 7289 gives an approximation to

accurate to nearly six decimal places.
Babylonian numerals The earliest evidence of written mathematics dates back to the ancient
Sumerians, who built the earliest civilization in Mesopotamia. They developed a complex system of
metrology from 3000 BC. From 2600 BC onwards, the Sumerians wrote
multiplication tables on clay tablets and dealt with
geometrical exercises and
division problems. The earliest traces of the Babylonian numerals also date back to this period.
Sumerian mathematics (3000-2300 BC) The
Old Babylonian period is the period to which most of the clay tablets on Babylonian mathematics belong, which is why the mathematics of Mesopotamia is commonly known as Babylonian mathematics. Some clay tablets contain mathematical lists and tables, others contain problems and worked solutions.
Old Babylonian mathematics (2000-1600 BC) The Babylonians made extensive use of pre-calculated tables to assist with
arithmetic. For example, two tablets found at Senkerah on the
Euphrates in
1854, dating from
2000 BC, give lists of the
squares of numbers up to 59 and the
cubes of numbers up to 32. The Babylonians used the lists of squares together with the formulas


to simplify multiplication.
The Babylonians did not have an algorithm for
long division. Instead they based their method on the fact that

together with a table of
reciprocals. Numbers whose only
prime factors are 2, 3 or 5 have finite reciprocals in sexagesimal notation, and tables with extensive lists of these reciprocals have been found.
Reciprocals such as 1/7, 1/11, 1/13, etc. do not have finite representations in sexagesimal notation. To compute 1/13 or to divide a number by 13 the Babylonians would use an approximation such as
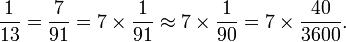 Arithmetic
Arithmetic As well as arithmetical calculations, Babylonian mathematicians also developed
algebraic methods of solving
equations. Once again, these were based on pre-calculated tables.
To solve a
quadratic equation the Babylonians essentially used the standard
quadratic formula. They considered quadratic equations of the form

where here
b and
c were not necessarily integers, but
c was always positive. They knew that a solution to this form of equation is

and they would use their tables of squares in reverse to find square roots. They always used the positive root because this made sense when solving "real" problems. Problems of this type included finding the dimensions of a rectangle given its area and the amount by which the length exceeds the width.
Tables of values of
n table to find the value closest to the right hand side. The Babylonians accomplished this without algebraic notation, showing a remarkable depth of understanding. However, they did not have a method for solving the general cubic equation.
Algebra The Babylonians may have known the general rules for measuring areas and volumes. They measured the circumference of a circle as three times the diameter and the area as one-twelfth the square of the circumference, which would be correct if
π is estimated as 3. The volume of a cylinder was taken as the product of the base and the height, however, the volume of the frustum of a cone or a square pyramid was incorrectly taken as the product of the height and half the sum of the bases. The
Pythagorean theorem was also known to the Babylonians. Also, there was a recent discovery in which a tablet used
π as 3 and 1/8. The Babylonians are also known for the Babylonian mile, which was a measure of distance equal to about seven miles today. This measurement for distances eventually was converted to a time-mile used for measuring the travel of the Sun, therefore, representing time.
Geometry There is also evidence that the Babylonians first used
trigonometric functions, based on a table of numbers written on the Babylonian
cuneiform tablet,
Plimpton 322 (circa 1900 BC), which can be interpreted as a table of secants.
Trigonometry Main article: Plimpton 322 Plimpton 322 Further information: Babylonian astronomy
Plimpton 322 Further information: Babylonian astronomy The
Neo-Babylonian Empire flourished during the
Chaldean period of Mesopotamia, which marked the second flowering of
Babylon as a capital city and center of study. This period provides the second source of Babylonian mathematics, though somewhat more vague than the Old Babylonian mathematics.
Since the rediscovery of the Babylonian civilization, it has become apparent that
Greek and
Hellenistic mathematicians and astronomers, and in particular
Hipparchus, borrowed a lot from the
Chaldeans.
Franz Xaver Kugler demonstrated in his book
Die Babylonische Mondrechnung ("
The Babylonian lunar computation", Freiburg im Breisgau, 1900) the following: Ptolemy had stated in his
Almagest IV.2 that Hipparchus improved the values for the Moon's periods known to him from "even more ancient astronomers" by comparing eclipse observations made earlier by "the Chaldeans", and by himself. However Kugler found that the periods that Ptolemy attributes to Hipparchus had already been used in Babylonian
ephemerides, specifically the collection of texts nowadays called "System B" (sometimes attributed to
Kidinnu). Apparently Hipparchus only confirmed the validity of the periods he learned from the Chaldeans by his newer observations.
It is clear that Hipparchus (and Ptolemy after him) had an essentially complete list of eclipse observations covering many centuries. Most likely these had been compiled from the "diary" tablets: these are clay tablets recording all relevant observations that the Chaldeans routinely made. Preserved examples date from
652 BC to
AD 130, but probably the records went back as far as the reign of the Babylonian king
Nabonassar: Ptolemy starts his chronology with the first day in the Egyptian calendar of the first year of Nabonassar, i.e.,
26 February 747 BC.
This raw material by itself must have been hard to use, and no doubt the Chaldeans themselves compiled extracts of e.g., all observed eclipses (some tablets with a list of all eclipses in a period of time covering a
saros have been found). This allowed them to recognise periodic recurrences of events. Among others they used in System B (cf.
Almagest IV.2):
The Babylonians expressed all periods in synodic
months, probably because they used a
lunisolar calendar. Various relations with yearly phenomena led to different values for the length of the year.
Similarly various relations between the periods of the
planets were known. The relations that Ptolemy attributes to Hipparchus in
Almagest IX.3 had all already been used in predictions found on Babylonian clay tablets.
All this knowledge was transferred to the
Greeks probably shortly after the conquest by
Alexander the Great (
331 BC). According to the late classical philosopher
Simplicius (early
6th century AD), Alexander ordered the translation of the historical astronomical records under supervision of his chronicler
Callisthenes of Olynthus, who sent it to his uncle
Aristotle. It is worth mentioning here that although Simplicius is a very late source, his account may be reliable. He spent some time in exile at the
Sassanid (Persian) court, and may have accessed sources otherwise lost in the West. It is striking that he mentions the title
tèresis (Greek: guard) which is an odd name for a historical work, but is in fact an adequate translation of the Babylonian title
massartu meaning "guarding" but also "observing". Anyway, Aristotle's pupil
Callippus of Cyzicus introduced his 76-year cycle, which improved upon the 19-year
Metonic cycle, about that time. He had the first year of his first cycle start at the summer solstice of
28 June 330 BC (
Julian proleptic date), but later he seems to have counted lunar months from the first month after Alexander's decisive battle at
Gaugamela in fall
331 BC. So Callippus may have obtained his data from Babylonian sources and his calendar may have been anticipated by Kidinnu. Also it is known that the Babylonian priest known as
Berossus wrote around
281 BC a book in Greek on the (rather mythological) history of Babylonia, the
Babyloniaca, for the new ruler
Antiochus I; it is said that later he founded a school of
astrology on the Greek island of
Kos. Another candidate for teaching the Greeks about Babylonian
astronomy/
astrology was
Sudines who was at the court of
Attalus I Soter late in the
3rd century BC.
In any case, the translation of the astronomical records required profound knowledge of the
cuneiform script, the language, and the procedures, so it seems likely that it was done by some unidentified Chaldeans. Now, the Babylonians dated their observations in their lunisolar calendar, in which months and years have varying lengths (29 or 30 days; 12 or 13 months respectively). At the time they did not use a regular calendar (such as based on the
Metonic cycle like they did later), but started a new month based on observations of the
New Moon. This made it very tedious to compute the time interval between events.
What Hipparchus may have done is transform these records to the
Egyptian calendar, which uses a fixed year of always 365 days (consisting of 12 months of 30 days and 5 extra days): this makes computing time intervals much easier. Ptolemy dated all observations in this calendar. He also writes that "All that he (=Hipparchus) did was to make a compilation of the planetary observations arranged in a more useful way" (
Almagest IX.2). Pliny states (
Naturalis Historia II.IX(53)) on eclipse predictions: "After their time (=
Thales) the courses of both stars (=Sun and Moon) for 600 years were prophesied by Hipparchus, …". This seems to imply that Hipparchus predicted eclipses for a period of 600 years, but considering the enormous amount of computation required, this is very unlikely. Rather, Hipparchus would have made a list of all eclipses from Nabonasser's time to his own.
Other traces of Babylonian practice in Hipparchus' work are:
223 (
synodic) months = 239 returns in anomaly (
anomalistic month) = 242 returns in latitude (
draconic month). This is now known as the
saros period which is very useful for predicting
eclipses.
251 (synodic) months = 269 returns in anomaly
5458 (synodic) months = 5923 returns in latitude
1
synodic month = 29;31:50:08:20 days (sexagesimal; 29.53059413… days in decimals = 29 days 12 hours 44 min 3⅓ s)
first Greek known to divide the circle in 360
degrees of 60
arc minutes.
first consistent use of the
sexagesimal number system.
the use of the unit
pechus ("cubit") of about 2° or 2½°.
use of a short period of 248 days = 9 anomalistic months.
Neo-Babylonian mathematics (626-539 BC) Main articles: Greek mathematics and Diophantus Babylonian mathematics in Alexandria Main article: Islamic mathematics
 accurate to nearly six decimal places.
accurate to nearly six decimal places.


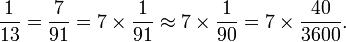


 Plimpton 322
Plimpton 322
No comments:
Post a Comment